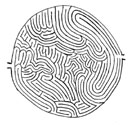
Unfortunately, most of the mazes that I have drawn have been lost over the years. But I recently started drawing and sketching again and I found that I miss drawing an occasional maze. I have only drawn a few since starting again but I plan to continue and draw many more. I've scanned a few of them into the computer and displayed them here. Please feel free to print them out and give them a try.


MODULAR MAZES
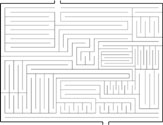
Below are examples of a new puzzle that I've been working on along with my brother, Chris. Each of these mazes is a perfect square. Each has four entry/exit points: one at the exact center of each side. However, as in the maze below, only two of the entry/exit points actually connect. You will have to try several approaches (north, south, east or west) to figure out which entry point has a route that goes all the way through to another exterior opening.

View the SOLUTION to this maze!
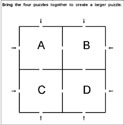
Okay, now here's the "modular" part. I can combine a group of four (or more) of these squares into an even larger maze. This new maze will then have eight (or more) exterior entry/exit points, but there will still be only one pair of exterior openings that can be connected via the maze. Other paths may lead you from one of the original square mazes into another, but they will not lead you to another exterior entry/exit of the larger puzzle. The examples below show how four smaller, square mazes can be put together to create one larger puzzle.

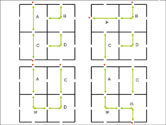
Remember that each original maze has only one route all the way through it, connecting only two exterior openings. (In the layout examples below, these connections are indicated by green arrows.) As shown below, the same four individual square mazes can be rearranged, and even individually rotated, to create many new puzzle configurations. Each of these larger puzzles will also have only two exterior openings that connect.
Someday, I might even make some of these squares that have multiple connections -- perhaps one square will have a path that can be successfully followed from north to south and a second, within the same square, that connects north to east. This should make the maze even harder to solve. And, of course, more squares can be added to make even larger, and more complex, square or rectangular puzzles.
The Modular Maze below was made by combining four copies of the same original puzzle. (Each quadrant of the puzzle is actually the same original puzzle rotated a different way.) Of course, in future puzzles, the individual squares will all be different. But, for now, this will give you an idea of how complex and interesting these puzzles can become. As you look at the example below try to imagine an even larger square made from nine (instead of only four) of the smaller puzzles. How about one made from sixteen? Sound confusing? Yeah, well... try drawing them.

View the SOLUTION to this maze!
I consider myself only an amateur puzzle-maker, but I enjoy making them nonetheless. I also enjoy solving mazes and other puzzles. If you would like to see, and try to solve, some really extraordinary mazes and puzzles, then visit:
"Clickmazes" is the website of British puzzle-maker, Andrea Gilbert. Her puzzles are terrific not only for their challenge and ingenuity but also for their artistry. You owe it to yourself to give her website a look. Enjoy!